Brief Aside. Sorry for the pause in Design Diary entries. In the final push to get Pedometer++ v5 submitted I ran out of time to keep them up. Never fear though I recorded a bunch of topic ideas to write about now that it has been submitted and I’m less pressured again.

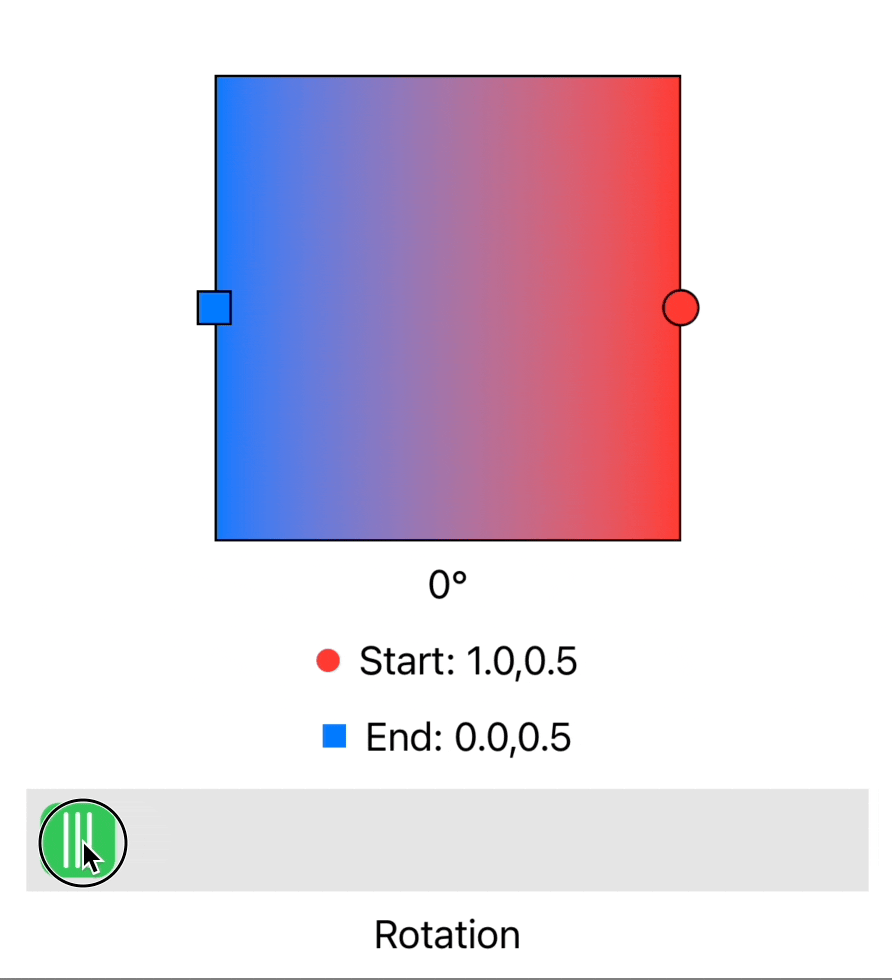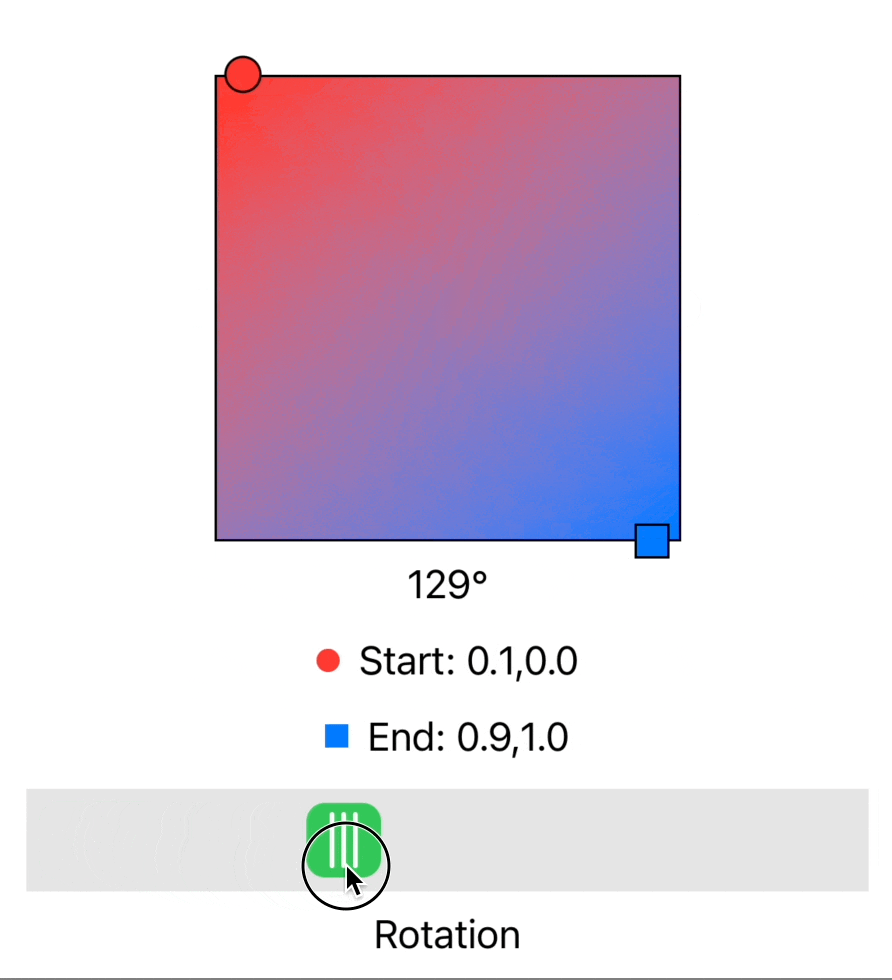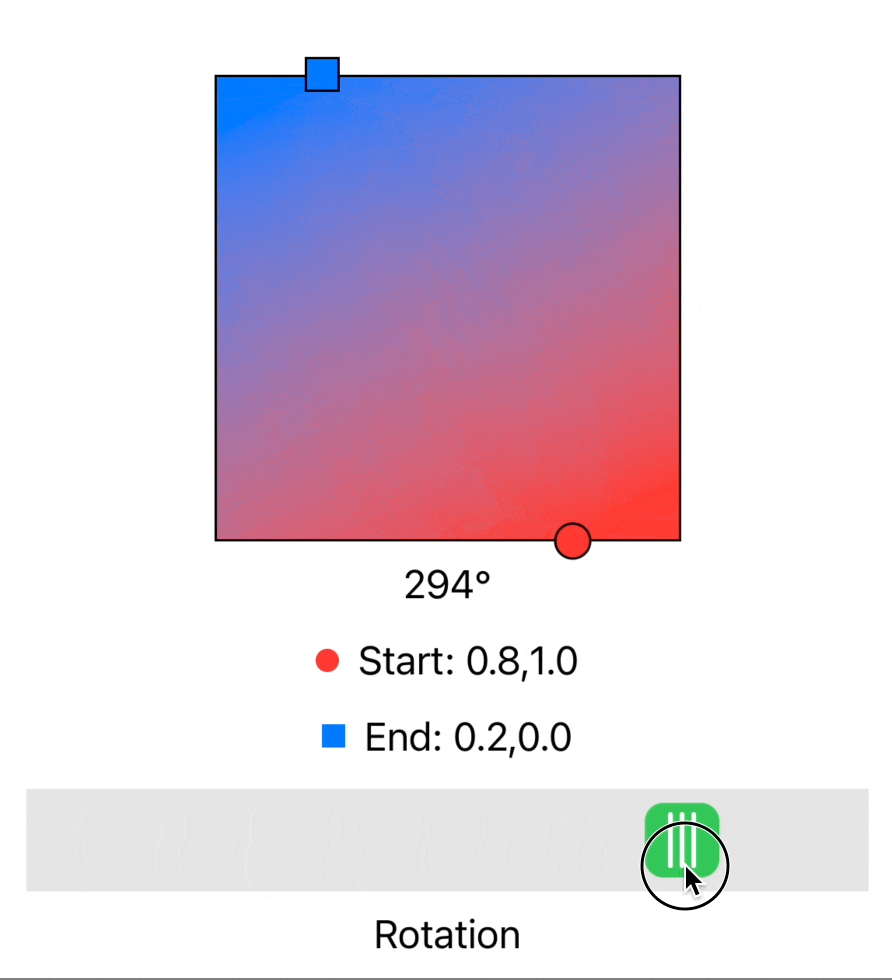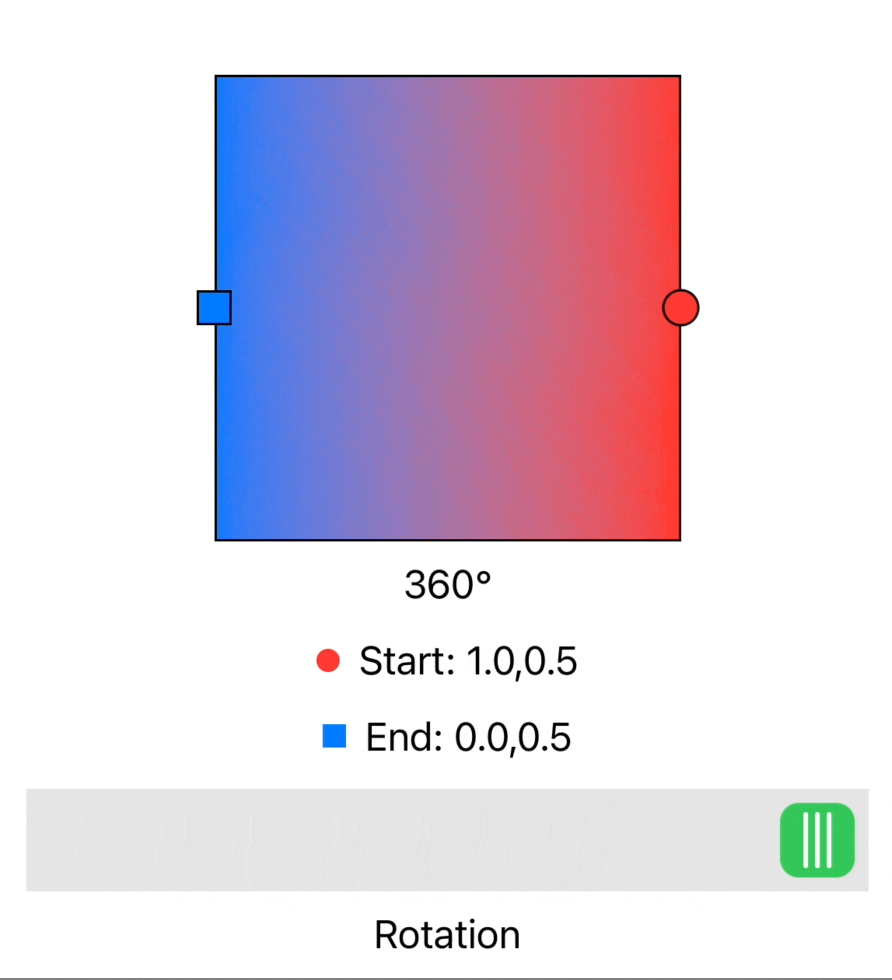
As part of an upcoming Widgetsmith feature I wanted to draw linear gradients. I’ve done this countless times using the wonderful LinearGradient fill style. This works great and can easily slot into so many different shapes and situations in SwiftUI.

Whenever I’ve used these before, however, I’ve only ever used the built-in direction values: .top, .topTrailing, .leading, etc. And if I’m being honest, those were the only options I thought we had.

For this particular feature I really wanted to be able to draw gradients at arbitrary angles rather than just horizontal, vertical and oblique. I started digging around a bit and to my delight discovered that this is actually already built into LinearGradient.

LinearGradient takes as its direction control an argument of type UnitPoint. Typically you interact with these using the built-in options but it turns out that this is just a normalized X/Y pair under the hood. So if I could workout the appropriate X/Y value I could draw my gradients at any angle.

Now the trick was working out how to calculate these pairs. I started out trying to do this with math(😱) and was quickly frustrated. I’m sure there is a clever, algebraic solution for this but I couldn’t find it after a bit of looking.

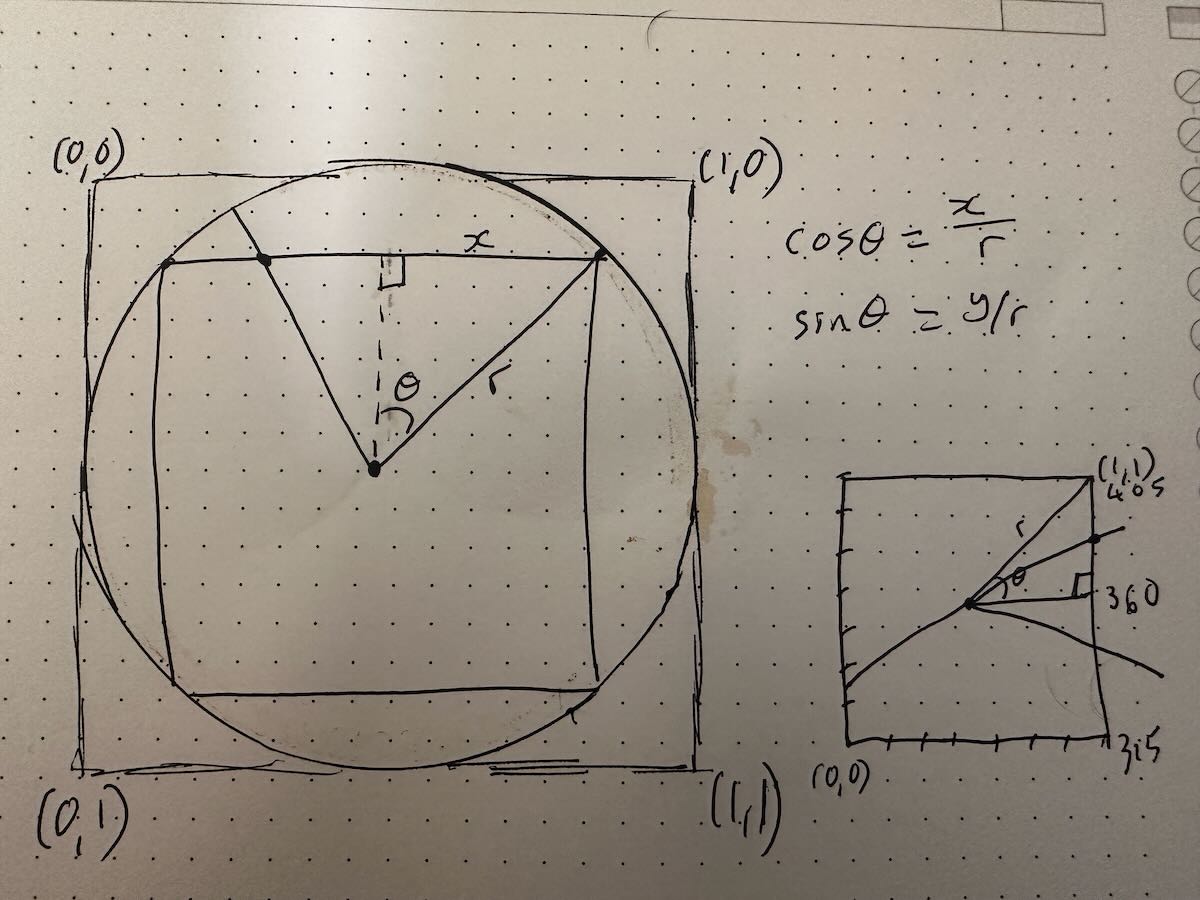
Then I realized that I could actually just simplify this whole thing since I only cared about one variable at a time (for example the Y-value on the left edge, and the X-Value on the bottom edge).

So I just took each edge in turn and calculated the relative proportion of the edge that it would have covered at a given angle. I just do this with a basic linear proportion calculation.

This works great and lets me draw gradients at any angle. If you’d like to see the code or use it yourself.

Here it is on GitHub.

Correction:

Rob Mayoff and robb pointed out to me that my method isn’t quite right. Because I’m doing a linear interpolation rather than a trigonometric one my rotations are slightly off from the actual angle. In this case the difference is tiny and visually very hard to differentiate but still, it isn’t quite right.

Here is the animation Rob made to illustrate this error:

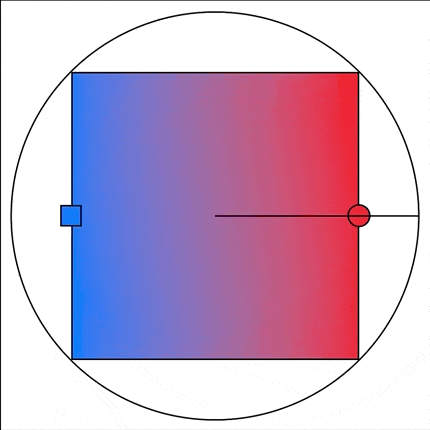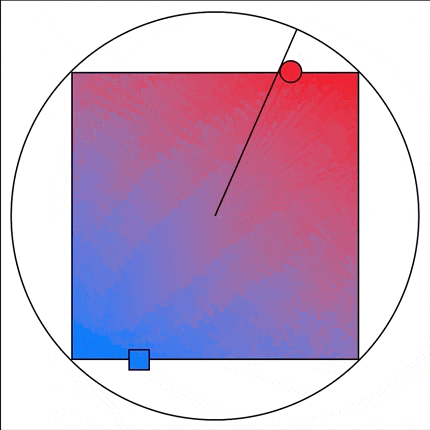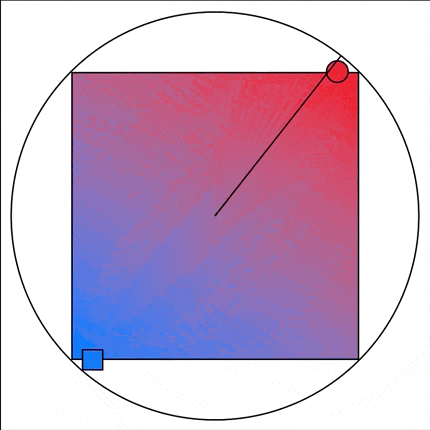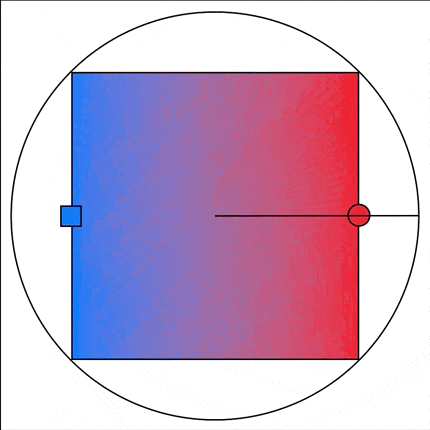
Rob and robb were kind enough to post their alternative solutions which correctly adjust for this.